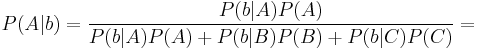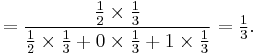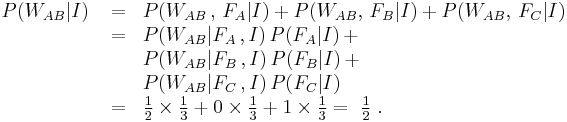Three Prisoners problem

The Three Prisoners problem appeared in Martin Gardner's Mathematical Games column in Scientific American in 1959.[1][2] It is mathematically equivalent to the Monty Hall problem with car and goat replaced with freedom and execution respectively, and also equivalent to, and presumably based on, Bertrand's box paradox.

Contents

Problem

Three prisoners, A, B and C, are in separate cells and sentenced to death. The governor has selected one of them at random to be pardoned. The warden knows which one is pardoned, but is not allowed to tell. Prisoner A begs the warden to let him know the identity of one of the others who is going to be executed. "If B is to be pardoned, give me C's name. If C is to be pardoned, give me B's name. And if I'm to be pardoned, flip a coin to decide whether to name B or C."

The warden tells A that B is to be executed. Prisoner A is pleased because he believes that his probability of surviving has gone up from 1/3 to 1/2, as it is now between him and C. Prisoner A secretly tells C the news, who is also pleased, because he reasons that A still has a chance of 1/3 to be the pardoned one, but his chance has gone up to 2/3. What is the correct answer?

Solution

The answer is that prisoner A didn't gain information about his own fate. Prisoner A, prior to hearing from the warden, estimates his chances of being pardoned as 1/3, the same as both B and C. As the warden says B will be executed, it's either because C will be pardoned (1/3 chance) or A will be pardoned (1/3 chance) and the B/C coin the warden flipped came up B (1/2 chance; for a total of a 1/6 chance B was named because A will be pardoned). Hence, after hearing that B will be executed, the estimate of A's chance of being pardoned is half that of C. This means his chances of being pardoned, now knowing B isn't, again are 1/3, but C has a 2/3 chance of being pardoned.

Mathematical formulation

Call A, B and C the events that the corresponding prisoner will be pardoned, and b the event that the warden mentions prisoner B as the one not being pardoned, then, using Bayes' formula, the posterior probability of A being pardoned, is:

P(A|b) = \frac{P(b|A)P(A)}{P(b|A)P(A)%2BP(b|B)P(B)%2BP(b|C)P(C)} =
=\frac{\tfrac12\times\tfrac13}{\tfrac12\times\tfrac13%2B0\times\tfrac13%2B1\times\tfrac13} = \tfrac13.

An intuitive explanation

Prisoner A only has a 1/3 chance of pardon. Knowing whether “B” or “C” will be executed does not change his chance. After he hears B will be executed, Prisoner A realizes that if he will not get the pardon himself it must only be going to C. That means there is a 2/3 chance for C to get a pardon.

Aids to understanding

As with the Monty Hall Problem, it may be useful to see this problem from alternative viewpoints for better understanding.

Bayesian analysis

An analysis using Bayesian probability theory begins by expressing the problem in terms of statements, or propositions, that may be true or false. Its goal is to compute the probability of these propositions, a number P in [0,1]\, measuring our confidence in their truth in light of all the background information available to us. The problem at hand concerns propositions of the form:

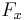F_x\, : "x will be pardoned", for x equal to one of A, B or C.
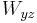W_{yz}\, : "Replying to y, the warden states that z is executed", for y and z equal to any of A, B or C.

For example, 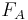\!\,F_A denotes the proposition "A will be pardoned", and 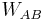W_{AB}\, denotes the proposition "Replying to A, the warden states that B is executed". In this context, "being pardoned" is the complement of "to be executed".

The background information consists of the rules of the game, henceforth denoted by 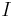I\,. They impose the following constraints on the probability of such propositions. First, the three prisoners have, a-priori, the same chance of being pardoned, hence the prior probability of 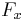\!\,F_x is:

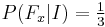P(F_x|I) = \tfrac13\, .

Second, the warden is truthful, and will always name as executed a prisoner other than the one questioning him. If he has a choice of two such prisoners, they are equally likely to be named in his response. This rule concerns the conditional probability of a proposition 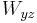W_{yz}\,, conditioned on a proposition F_x\, and I\,:

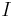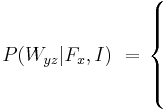
P(W_{yz} | F_x, I)\,\, =\,\begin{cases} \, \\ \, \\ \, \\ \, \end{cases} \!\,0   if y = z, (the warden shall not reveal the asking prisoner that he is executed)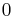
\!\,0   if z = x, (the warden shall not lie, by indicating as executed a prisoner that, in fact, is to be pardoned)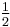
\!\,\tfrac 12   if y = x, (the prisoner who asks is to be pardoned, and the warden names either one of the others as executed)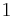
\!\,1   if y ≠x and y ≠ z, (prisoner z is the only one the warden can mention in reply)

Now assume, by renaming the prisoners if necessary, that A is the one questioning the warden, and B the one the warden names as executed. After the warden's reply, A's opinion about his chances of being pardoned are expressed by the posterior probability 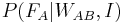P(F_A | W_{AB}, I)\,. Using Bayes' theorem this is expressed as:

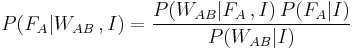P(F_A|W_{AB}\,, I) = \frac{P(W_{AB}| F_A\,, I) \, P(F_A | I)}{P(W_{AB} | I)} .

By the rules stated above, the numerator of the right-hand side is:

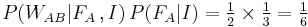P(W_{AB}| F_A\,, I) \, P(F_A | I) = \tfrac12 \times \tfrac13 = \tfrac16 .

The normalizing constant at the denominator can be evaluated by expanding it using the Law of total probability:

\begin{array}{lcl} P(W_{AB}|I) &{}= &P(W_{AB}\,,\,F_A|I) %2B P(W_{AB},\,F_B|I) %2B P(W_{AB},\,F_C|I) \\ &{}= &P(W_{AB}|F_A\,,I) \, P(F_A|I)\, %2B \\ &&P(W_{AB}|F_B\,,I) \, P(F_B|I)\, %2B \\ &&P(W_{AB}|F_C\,,I) \, P(F_C|I) \\ &{}= &{\displaystyle \tfrac12 \times \tfrac13 %2B 0 \times \tfrac13 %2B 1 \times \tfrac13} = \ {\displaystyle\tfrac12\ .} \end{array}

Dividing the numerator by the normalizing constant yields:

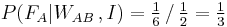P(F_A|W_{AB}\,,I) = \tfrac16\,/\,\tfrac12 = \tfrac13 .

As the value of the posterior probability is equal to the prior one, this shows that the warden has given no additional information concerning A 's fate . Further, since B is executed, it is 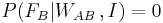P(F_B | W_{AB}\,,I) = 0. Hence the chances that C is to be pardoned are, in A's opinion,

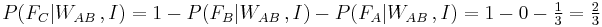{\displaystyle P(F_C | W_{AB}\,,I) = 1 - P(F_B | W_{AB}\,,I) - P(F_A|W_{AB}\,,I) = 1 - 0 - \tfrac13 = \tfrac23}.

Therefore A must judge it safer to try switch his fate with C 's.

Enumeration of possible cases

The following scenarios may arise:

  1. A is pardoned and the warden mentions B to be executed: 1/3×1/2=1/6 of the cases
  2. A is pardoned and the warden mentions C to be executed: 1/3×1/2=1/6 of the cases
  3. B is pardoned and the warden mentions C to be executed: 1/3 of the cases
  4. C is pardoned and the warden mentions B to be executed: 1/3 of the cases

With the stipulation that the warden will choose randomly, in the 1/3 of the time that A is to be pardoned, there is a 1/2 chance he will say B and 1/2 chance he will say C. This means that taken overall, 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says B]), the warden will say B because A will be pardoned, and 1/6 of the time (1/3 [that A is pardoned] * 1/2 [that warden says C]) he will say C because A is being pardoned. This adds up to the total of 1/3 of the time (1/6 + 1/6) A is being pardoned, which is accurate.

It is now clear that if the warden answers B to A, cases 1 and 4, which happens 1/2 of the time, 1/3 of the time C is pardoned and A will still be executed (case 4), and only 1/6 of the time A is pardoned (case 1). Hence C's chances are (1/3)/(1/2)=2/3 and A's are (1/6)/(1/2)=1/3.

The key to this problem is that the warden may not reveal the name of a prisoner who will be pardoned. If we eliminate this requirement, it can demonstrate the original problem in another way. The only change in this example is that prisoner A asks the warden to reveal the fate of one of the other prisoners (not specifying one that will be executed). In this case, the warden flips a coin chooses one of B and C to reveal the fate of. The cases are as follows:

  1. A pardoned, warden says: B executed (1/6)
  2. A pardoned, warden says: C executed (1/6)
  3. B pardoned, warden says: B pardoned (1/6)
  4. B pardoned, warden says: C executed (1/6)
  5. C pardoned, warden says: B executed (1/6)
  6. C pardoned, warden says: C pardoned (1/6)

Each scenario has a 1/6 probability. The original Three Prisoners problem can be seen in this light: The warden in that problem still has these six cases, each with a 1/6 probability of occurring. However, the warden in that case may not reveal the fate of a pardoned prisoner. Therefore, in the 1/6 of the time that case 3 occurs, since saying B is not an option, the warden says C instead (making it the same as case 4). Similarly, in case 6, the warden must say B instead of C (the same as case 5). That leaves cases 4 and 5 with 1/3 probability of occurring and leaves us with the same probability as above.

Why the paradox?

The tendency of people to provide the answer 1/2 neglects to take into account the query that the warden was asked. Had the query been: "Will B be executed?" then the warden's answer "Yes, B will be executed" would indeed result in a probability 1/2 for A's death. Judea Pearl (1988)[3] used a variant of this example to demonstrate that belief updates must depend not merely on the facts observed but also on the experiment (i.e., query) that led to those facts.

Related problems and applications

Notes

  1. ^ Gardner, Martin (1959a). "Mathematical Games" column, Scientific American, October 1959, pp. 180–182.
  2. ^ Gardner, Martin (1959b). "Mathematical Games" column, Scientific American, November 1959, p. 188.
  3. ^ Pearl, J. Probabilistic Reasoning in Intelligent Systems: Networks of Plausible Inference, San Mateo, CA: Morgan Kaufmann Publishers, Inc., First Edition, 1988.

References